方差离散图
- 版本 :Minitab 21
方差离散图
此宏可在给定特定模型的情况下为多达五个设计矩阵计算缩放预测方差。您可以评估某个设计的缩放预测方差、评估某个设计的旋转情况,并比较设计以确定预测方差在设计空间的行为情况。这将可让您在收集任何 DOE 数据之前按编码单位及其性能比较设计。这些设计限于 2 个或更多因子。
下载宏
确保 Minitab 知道可在何处找到您下载的宏。选择。在宏位置下,浏览到您保存宏文件的位置。
重要信息
如果您使用较低版本的 Web 浏览器,则在您单击下载按钮时,此文件可能会在 Quicktime 中打开,因为 Quicktime 与 Minitab 宏使用相同的 .mac 文件扩展名。要保存此宏,请右键单击下载按钮并选择目标另存为。
必需输入
您最多需要五个设计矩阵。
可选输入
MODEL 模型类型
指定要在运行试验时检验的模型。默认设置是“交互”。您可以输入多种模型,如线性模型、二次模型、交互模型、纯二次模型。每个模型包括以下项:
线性模型:常量和线性项
交互模型:常量、线性和交叉乘积项
二次模型:交互和平方项
纯二次模型:常量、线性和平方项
RESOLUTION K
用于指定采样设计点的数量,这些采样设计点用于估计最小值、最大值以及半径内每个可区分值的综合预测方差。对于可旋转的设计,可选择较小的分辨率。对于不可旋转的设计,可能需要随着因子数的增加而提高分辨率。默认为 500 个设计点。
INCREMENT K
用于指定半径增量。您可以更改此值以采用更高或更低的分辨率显示图形。默认值为 0.1 个编码单位。
MAXDIST K
表示最大半径距离。默认情况下,此值定义为与距设计中心最远的设计点之间的最大距离。对于基于多个设计的 VDG,MAXDIST 设置为距所有设计的最大距离。
运行宏
假设已将 CCD 的一个因子复制到矩阵 M1,并且 Box-Behnken 设计的因子已存储在 M2 中。要运行此宏,请选择,然后键入:
%VDG M1 M2; MODEL "quadratic"; RESOLUTION 150。
单击运行。
更多信息
方差离散图和实验设计
方差离散图是一种在选择试验设计 (DOE) 的过程中使用的图形工具。这些图形显示了 DOE 在整个设计空间中的缩放预测方差,通常用于比较响应曲面设计。不过,方差离散图也可用于比较某一特定模型(如线性模型、带交互作用项的线性模型、带二次项的线性模型或完全二次模型)的多种设计所具备的性能。
VDG 的历史和背景
VDG 最初是由 Giovannitti-Jensen 和 Myers (1989) 以及 Myers 等人 (1992) 开发的,用于显示设计空间内缩放预测方差的稳定性快照。
在数学上,可使用下面的等式估计缩放的预测方差:
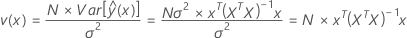
其中,v(x) 是点 x 处的缩放预测方差,并且如上所示,并不依赖于响应数据,而是只依赖于设计矩阵 X。也就是说,缩放预测方差是您的试验、协方差矩阵和评估预测方差的点处的游程数的函数。由于 VDG 显示的缩放预测方差不依赖响应数据,因此 VDG 可以让您评估先验设计的优度。
在一般情况下,一个 VDG 由四个基本分量构成:
球面方差与半径 r 的关系图。球面方差是半径为 r 的球体表面的平均(综合)v(x)。
· 对于从原点开始的多个 r 值,半径 r 的最大预测方差的图形(r 开始于零点,然后按小的增量步阶,直到达到离原点最远的设计点)。
· 对于从原点开始的多个 r 值,半径 r 的最小预测方差的图形。
v(x) = p 处的水平线,其中 p 是要拟合的模型中的参数个数。“最优”设计的最大预测方差小于或等于设计空间内所有点的 p。
VDG 会显示不同 r 值情况下的平均、最大、最小缩放预测方差,其表示任何给定点与设计原点或中心的距离。
使用 VDG 评估设计的其他方面
使用 VDG,可以用单个设计的预测方差来评估该设计的性能。您还可以使用 VDG 来比较两个或更多设计。VDG 的另一个应用是评估向设计中添加中心点的效应。
您还可以使用 VDG 评估设计是否可旋转。在可旋转的设计中,图形中的所有三条线(最小值、平均值和最大值)都将重合。如果最小值、平均值和最大值线不重合,那么表面中心设计不可旋转。
用于估计预测方差的蒙特卡罗模拟法
此高级部分描述用来估计 VDG 中所显示的最小预测方差、最大预测方差和平均预测方差的数学方法。如果您仅对如何通过运行宏来显示和解释 VDG 感兴趣,则可能希望跳过此部分。
如前所述,对于固定的半径值,需要执行搜索来找出最小、最大和综合的缩放预测方差。为 Minitab 宏所选择的方法基于蒙特卡罗模拟法以及从设计的中心 x = (0,0,…,0)T 开始的等距点上进行一致搜索的功能。
共有三个量需要在与原点的不同距离上进行计算:1) 最小预测方差,2) 最大预测方差,以及 3) 综合预测方差。可通过多种方法找到这些量。其中一种方法是使用非线性的编程算法来查找最小和最大预测方差。但是,我们选择的估计这些量的方法是先进行一致的采样,然后为不同的 r 值找出与设计中心距离相同的较大一组可区分点。在等距点空间中,可以通过满足两项条件来保证对最小和最大预测方差作出恰当的估计:首先,等距点需要均匀采样。也就是说,不能有任何区域的等距点存在比其他区域中的等距点更高的被选择概率。第二,点的数量需足够多才能覆盖可能存在设计点的整个区域。
因为所有需采样的点是等距的,所以采样问题等同于寻找用于从 n-ball 或超球面针对给定半径获取点的最佳方法。
该过程由 Marsaglia 描述(1972 年),摘要如下:
生成正态随机变量的 n 维向量(例如,从标准正态分布)。设此向量为 x = (x1, x2,…,xn)。创建多个向量 x。
为所有已生成的点 x 计算半径 ρ。

转换在步骤 1 中得到的每一个原始设计点,方法是将矢量 x 的每个条目乘以 r,其中 r 代表要从中采样的超球面的半径。
现在,我们已经阐述了在半径为常量 r 的超球面中对点进行抽样的方法。我们可以使用该抽样方法来估计最大或最小预测方差。借助这些样本,根据弱大数定律,只要 n 足够大,就可以将抽取的设计点的平均预测方差用于估计真正的综合预测方差。
参考资料
[1] Marsaglia G。“Choosing a Point from the Surface of a Sphere”(从球面中选择点)。The Annals of Mathematical Statistics(数理统计年鉴),第 43 卷第 2 期 (1972), 第 645 到 646 页。
[2] Myers R, Montgomery D。(2002)。“Response Surface Methodology - Process and Product Optimization Using Designed Experiments”(响应曲面方法:利用设计试验优化过程和产品)(第二版)。John Wiley & Sons, Inc.




