Kruskal Wallis 多重比较
- 版本 ：Minitab 21
Kruskal Wallis 多重比较
Kruskal Wallis H 统计量是一个整体检验统计量，支持对所有总体中位数相等情况下的一般假设进行检验。通常情况下，调查者对于这个一般假设不太感兴趣，而会对比较各个组感兴趣。此宏可在非参数设置中执行多重比较。
下载宏
确保 Minitab 知道可在何处找到您下载的宏。选择。在宏位置下，浏览到您保存宏文件的位置。
重要信息
如果您使用较低版本的 Web 浏览器，则在您单击下载按钮时，此文件可能会在 Quicktime 中打开，因为 Quicktime 与 Minitab 宏使用相同的 .mac 文件扩展名。要保存此宏，请右键单击下载按钮并选择目标另存为。
必需输入
一列数值响应数据
一列对应因子水平
注意
您可以通过指定 UNSTACKED 子命令来使用非堆叠数据。
可选输入
UNSTACKED
指定数据是否为非堆叠数据。
FALPHA
用于指定所需的整体 alpha 水平（默认值是 .20）。
CONTROL C
用于指定要控制的列 (C)。
注意
如果数据为堆叠数据，则控制组的响应不得与其他因子水平的响应在同一列中。控制组的响应必须在单独的列中。
运行宏
假设响应数据在 C1 中，因子水平在 C2 中。要运行此宏，请选择，然后键入以下内容：
%KRUSMC C1 C2
单击运行。
输出
输出内容的第一部分将显示所生成的比较数 (k)
、整体 alpha (α)、Bonferroni 个体 alpha (β)
，以及双侧临界 z 值。
下一部分显示了与这些差关联的标准化组均值秩差 (θ) 和 p 值。请注意，这些表格是对称的，所以在其顶部的三角形部分中有星号。同样，在沿表格对角线的位置处还有一些零，这是因为对角线表示组和其自身的比较（这些比较没有意义，在分析中并不考虑在内）。有关如何阅读此表格的示例如下：组 2 和组 4 之间的差值是多少？第三部分显示了中位数的符号置信区间。这些区间的置信水平按照整体 alpha 进行控制。由于这些区间按照全族的整体 alpha 进行控制，因此我们可以采用配对的方式比较这些区间（附录 2）。务必记住，希望得到的置信度可能无法在所有或部分区间上实现。此外，这种通过全族 alpha 实现的“整体”覆盖在样本数量不同的情况下并不准确，但通常还是能达到合理的近似程度。
最后一部分显示了如何才能算作“显著”的差（如果存在的话）。此部分中展示了 z 值、临界 z 值以及和 z 值关联的 p 值。
此图显示了标准化非绝对组均值秩差。在此图中，我们不仅可以看到组差的大小，还可以看到组差的方向，因此非常有用。它还显示了正临界 z 值和负临界 z 值，因此您可以查看差是否“显著”。
数据中的结
如果数据中存在结，则会计算出无偏常量（或校正因子）2。H 统计量随后将调整为 3。标准差 (ξ) 也将根据校正因子 4 进行调整。输出将同时显示调整后和未调整的表格。但是，只会给出调整后的表格的 p 值，因为这些才是应该使用的表格。显示未调整表格的主要原因在于显示结对于 z 值产生的效果。如果结非常广泛，则应当质疑数据的有效性，因为这些检验假定分布是连续的。通常情况下，结只会对您的结论造成很小的影响，或者完全没有影响。
鸣谢
非常感谢 Tom Hettmansperger 博士（宾夕法尼亚州立大学），他对此宏进行了审阅，并针对这项工作进行了多次讨论，付出了宝贵时间和热心帮助。另外，也感谢 Nicholas Bolgiano 先生和 Mike Delozier 先生 (Minitab, Inc.)
其他信息
Dunn 提出的检验
Dunn (1964) 提出了一种高效执行配对联立推导的方式。我们首先将数据合并，然后进行排秩，找出组均值秩，进而获得这些平均秩的标准化绝对差。
设 k = 处理次数，
设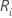 
= 第 i 个处理的秩的总和，i = 1,…,k
设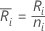 
其中，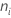
= 第 i 个处理的观测值数目。
设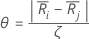 
其中 j=l,...,k 和 j 
i
其中，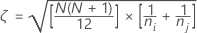
H 统计量
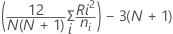
其中，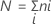
然后，在下列情况下我们将声明“显著性：
其中，
其中，α 是指定的整体 alpha 值，